Principe Fondamentale de la Statique (PFS)
Définition : Mécanique des solides
La mécanique des solides s'intéresse à plusieurs volets du comportement des structures des systèmes :
la statique (étude de l'équilibre des corps ex : fondations, actions aux appuis d'une structure porteuse, recherche d'effort de serrage d'une pince...)
la cinématique (étude des vitesses d'un solide en mouvement)
la dynamique (étude des efforts sur un solide en mouvement accéléré : ex dossier de siège de voiture...)
la Résistance des Matériaux (étude de la déformation des corps soumis à des efforts ex : charpente, dimensions d'une bride en phase de serrage...)
1) Hypothèses simplificatrices : cas particuliers des problèmes plans
Pour de nombreux systèmes mécaniques étudiés en Statique, on peut modéliser le système de la même manière que s'il était plan. Pour cela, il faut respecter certaines conditions :
le système mécanique admet un plan de symétrie dans la géométrie du système
les actions mécaniques de type « glisseur » sont comprises dans ce plan
les actions mécaniques de type « moment » sont perpendiculaires à ce plan de symétrie.
Généralisation
Tous les torseurs sont alors simplifiés de la façon suivante :
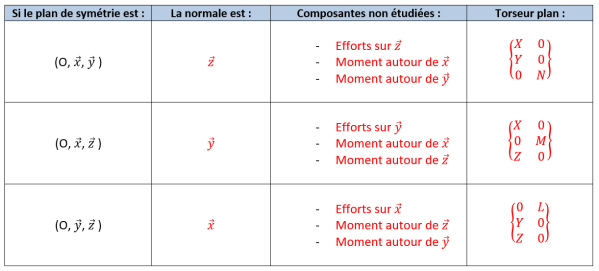
2) Conditions d'équilibre – Enoncé du Principe Fondamental de la Statique (PFS)
Hypothèses :
la masse des solides reste constante dans le temps
les solides sont supposés indéformables
Définition : Principe Fondamentale de la Statique
Un solide (ou un ensemble de solides) est en équilibre si la somme des forces extérieures qui lui sont appliquées ET la somme des moments de celles-ci sont nulles.
Cela se traduit par l'écriture des deux théorèmes suivant :
Théorème de la résultante statique :la somme des actions mécaniques extérieures exercées sur le solide isolé est nulle
Théorème du moment statique : la somme des moments en un point A quelconque est nulle
Remarque :
L'énoncé précédent est également vérifié pour des solides dont le mouvement est effectué sans accélération (cas particulier du Principe Fondamental de la Dynamique)
2-1) Principe des actions mutuelles :
Pour deux solides 0 et 1 en contact, l'action exercée par le solide 1 sur le solide 0 est égale et opposée à l'action du solide 0 sur le solide 1.
 | P.A.M en A : |
Définition : 2-2) Cas d'un solide soumis à 2 forces :
Un solide soumis à deux forces est en équilibre si et seulement si ces deux forces ont :
le même support
la même norme
des sens opposés
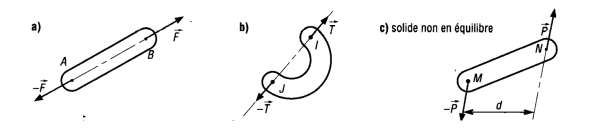
Définition : 2-3) Cas d'un solide soumis à 3 forces coplanaires non parallèles :
Dans le cas d'un solide soumis à 3 forces coplanaires non parallèles, d'après le Principe Fondamental de la Statique, l'équilibre s'obtient lorsque ces trois forces sont concourantes et leur somme vectorielle est nulle.
Il faut pour cela connaître au moins un support et une force entièrement définie.
Exemple : Abri de RER
Le dispositif se compose essentiellement d'un tirant 2 et d'une toiture 1.
Hypothèses et Données
Les liaisons en A, B et C sont des liaisons pivots d'axe . Elles sont supposées parfaites. On néglige les frottements
Seul le poids de la toiture (1) est pris en compte. Celui du tirant 2 est négligé.
Le tirant est placé dans le plan de symétrie géométrique de la toiture.
La toiture (1) a une masse de 1000kg. On prendra g=9.81m/s².
Méthode : Déterminer les actions exercées sur le tirant 2 dans le but de le dimensionner.
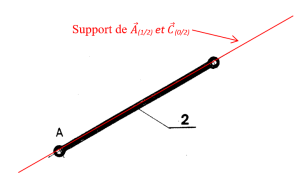
1) Isoler le tirant 2
PFS sur un solide soumis à deux forces :
donc on en déduit que le support de |  |
2) Isoler la toiture 1
Échelle des forces :10 mm ==> 4 000 N
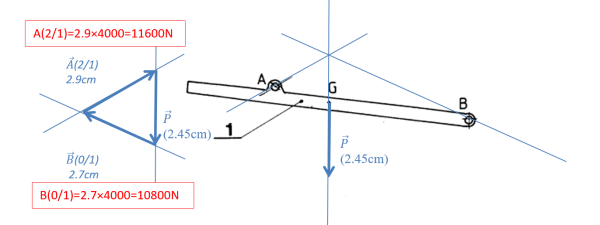
P.A.M en A : 
= - 
donc même support (AC)
Force | Point d'application | Direction | Sens | Norme |
| A | [AC] | ? | ? |
| B | ? | ? | ? |
| G | verticale | ↓ | 9 810 N |
On constate que l'on a un solide à l'équilibre sous l'action de trois forces. On connaît une force entièrement (
) et que l'on connaît le support de : (AC). On peut donc appliquer le PFS graphique.
1) Théorème du moment statique : 
→ On trouve le point I et on en déduit le support de 
2) Théorème de la résultante statique : + + = 
→ On trace le dynamique des forces afin de déterminer tous les vecteurs
On trouve la longueur des vecteurs en mesurant sur le dynamique des forces et on passe par l'échelle pour avoir la norme.
Conclusion :
Exemple : 2-4) Cas d'un solide soumis à des forces parallèles :
Formule Renault
Hypothèses :
Cette étude sera menée dans le plan longitudinal de symétrie (O,X ⃗,Y ⃗ ).
On supposera que le contact entre les roues et le sol en H et J, est un contact ponctuel de normale Y .
Données:
a = 1500 mm b = 900 mm h = 300 mm g = 9.81m/s² M = 500 Kg.
Objectif : Déterminer les actions exercées sur les roues pour dimensionner les amortisseurs.
→ Isoler la voiture et tracer un représentant vectoriel des forces sur la figure ci-dessus.
Force | Point d'application | Direction | Sens | Norme |
| H | verticale | ↑ | ? |
| J | verticale | ↑ | ? |
| G | verticale | ↓ | 4 905N |
→Appliquer le PFS au point J et déterminer les inconnues.
Théorème de la résultante statique : 
donc /y : H(0/1)+J(0/1)-P=0
Théorème du moment statique : 
donc /z : -
×2.4+0+4 905×0.9=0
donc =1 839.37N et avec la première équation : 
=-= 4 905-1 839.37=3 065.63N.
